Draw a Circle With Python

Describe Circle — Diameter, Radius, Arc and Segment Using Python Matplotlib Module

In this blog, we will plot indicate at origin then circle. Afterward that nosotros volition plot bore, radius, arc and segment(chord) using Matplotlib library.

Created by Nutan

Information most circles

Circle

A circle is a shape consisting of all points in a plane that are at a given distance from a given signal, the centre; equivalently it is the curve traced out by a point that moves in a plane so that its altitude from a given point is abiding. The altitude between any point of the circumvolve and the center is chosen the radius.

Circumference

The distance around the circumvolve.

Center

The bespeak equidistant from all points on the circumvolve.

Bore

Bore a line segment whose endpoints lie on the circumvolve and that passes through the center; or the length of such a line segment. This is the largest distance between any two points on the circumvolve.

Radius

The distance between any point of the circle and the heart is called the radius.

Arc

whatever connected part of a circle. Specifying two end points of an arc and a center allows for ii arcs that together brand upwardly a full circle.

Chord

A line segment whose endpoints prevarication on the circumvolve, thus dividing a circle into two segments.

Import Modules

                      import matplotlib.pyplot as plt
import numpy as np
from numpy import sin, cos, pi, linspace                  

Plot point at origin(0, 0)

                      #draw point at origin (0, 0)
plt.plot(0,0, color = 'red', marking = 'o')
plt.show()                  

Output:

Point at origin(0, 0)

Add annotation and set xlim and ylim

          #draw bespeak at origin (0, 0)
plt.plot(0,0, color = 'red', mark = 'o')
            plt.gca().annotate('O (0, 0)', xy=(0 + 0.1, 0 + 0.ane), xycoords='data', fontsize=10)                                plt.xlim(-2, two)
plt.ylim(-ii, 2)
plt.gca().set_aspect('equal')            
plt.testify()        

Output:

Bespeak with annotaion

Draw a circumvolve

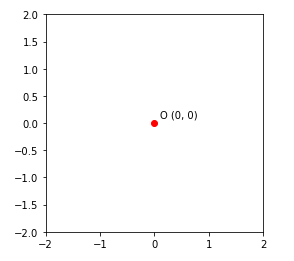
          #describe point at origin (0, 0)
plt.plot(0,0, color = 'scarlet', marking = 'o')
plt.gca().comment('O (0, 0)', xy=(0 + 0.1, 0 + 0.ane), xycoords='information', fontsize=ten)                      #draw a circumvolve
angles = linspace(0 * pi, 2 * pi, 100 )                                xs = cos(angles)
ys = sin(angles)                                plt.plot(xs, ys, colour = 'green')                    plt.xlim(-2, two)
plt.ylim(-two, ii)
plt.gca().set_aspect('equal')
plt.prove()        

Output:

Cicle

Increase circle radius from 1 to 1.5

          plt.plot(0,0, color = 'cherry', mark = 'o')
plt.gca().annotate('O (0, 0)', xy=(0 + 0.1, 0 + 0.one), xycoords='data', fontsize=10)          #describe a circumvolve
angles = linspace(0 * pi, 2 * pi, 100 )
            r = i.5
xs = r * cos(angles)
ys = r * sin(angles)                    plt.plot(xs, ys, color = 'green')          plt.xlim(-two, ii)
plt.ylim(-two, 2)
plt.gca().set_aspect('equal')
plt.prove()        

Output:

Circle with radius one.5

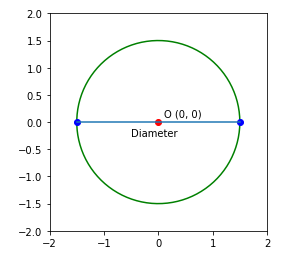
Draw diameter of circle

          #draw point at orgin
plt.plot(0,0, colour = 'ruddy', marker = 'o')
plt.gca().annotate('O (0, 0)', xy=(0 + 0.1, 0 + 0.one), xycoords='data', fontsize=10)          #draw a circle
angles = linspace(0 * pi, 2 * pi, 100 )
r = ane.5
xs = r * cos(angles)
ys = r * sin(angles)          plt.plot(xs, ys, colour = 'greenish')                      #draw daimeter
plt.plot(1.5, 0, marking = 'o', color = 'blueish')
plt.plot(-1.5, 0, mark = 'o', color = 'blue')
plt.plot([1.five, -i.five], [0, 0])
plt.gca().annotate('Diameter', xy=(-0.v, -0.25), xycoords='data', fontsize=ten)                    plt.xlim(-2, 2)
plt.ylim(-2, two)
plt.gca().set_aspect('equal')
plt.evidence()        

Output:

Diameter

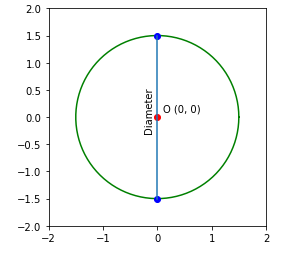
Describe diameter from 90 degree

          #describe point at orgin
plt.plot(0,0, colour = 'red', marker = 'o')
plt.gca().annotate('O (0, 0)', xy=(0 + 0.1, 0 + 0.1), xycoords='data', fontsize=ten)          #draw circumvolve
angles = linspace(0 * pi, 2 * pi, 100 )
r = one.5
xs = r * cos(angles)
ys = r * sin(angles)          plt.plot(xs, ys, color = 'green')          #draw daimeter
            plt.plot(0, 1.5, marking = 'o', color = 'blueish')
plt.plot(0, -i.five, mark = 'o', color = 'blue')
plt.plot([0, 0], [i.v, -1.five])
plt.gca().annotate('Diameter', xy=(-0.25, -0.25), xycoords='data', fontsize=10, rotation = ninety)                    plt.xlim(-two, two)
plt.ylim(-two, ii)
plt.gca().set_aspect('equal')
plt.show()        

Output:

Diameter

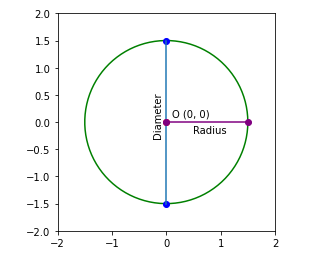
Describe radius

          #describe bespeak at orgin
plt.plot(0,0, color = 'red', marking = 'o')
plt.gca().comment('O (0, 0)', xy=(0 + 0.1, 0 + 0.1), xycoords='information', fontsize=ten)          #draw circle
r = one.5
angles = linspace(0 * pi, ii * pi, 100 )
xs = r * cos(angles)
ys = r * sin(angles)          plt.plot(xs, ys, color = 'light-green')          #draw daimeter
plt.plot(0, 1.five, marker = 'o', colour = 'blue')
plt.plot(0, -one.five, marker = 'o', colour = 'bluish')
plt.plot([0, 0], [i.5, -one.5])
plt.gca().annotate('Diameter', xy=(-0.25, -0.25), xycoords='information', fontsize=x, rotation = 90)                      #draw radius
plt.plot(0, 0, marking = 'o', color = 'majestic')
plt.plot(ane.five, 0, marker = 'o', color = 'imperial')
plt.plot([0, i.five], [0, 0], color = 'regal')
plt.gca().annotate('Radius', xy=(0.5, -0.2), xycoords='information', fontsize=x)                    plt.xlim(-2, ii)
plt.ylim(-2, 2)
plt.gca().set_aspect('equal')
plt.testify()        

Output:

Radius

Depict arc from 0 to pi/4

          #describe indicate at orgin
plt.plot(0,0, color = 'red', marker = 'o')
plt.gca().comment('O (0, 0)', xy=(0 + 0.1, 0 + 0.1), xycoords='information', fontsize=10)          #depict circumvolve
r = 1.v
angles = linspace(0 * pi, 2 * pi, 100 )
xs = r * cos(angles)
ys = r * sin(angles)          plt.plot(xs, ys, color = 'light-green')          #draw daimeter
plt.plot(0, 1.5, marking = 'o', color = 'blue')
plt.plot(0, -1.five, mark = 'o', color = 'bluish')
plt.plot([0, 0], [1.v, -1.5])
plt.gca().annotate('Diameter', xy=(-0.25, -0.25), xycoords='data', fontsize=ten, rotation = 90)          #draw radius
plt.plot(0, 0, marker = 'o', color = 'imperial')
plt.plot(1.5, 0, marker = 'o', colour = 'purple')
plt.plot([0, one.5], [0, 0], colour = 'purple')
plt.gca().annotate('Radius', xy=(0.5, -0.2), xycoords='data', fontsize=x)                      #draw arc
arc_angles = linspace(0 * pi, pi/4, 20)
arc_xs = r * cos(arc_angles)
arc_ys = r * sin(arc_angles)
plt.plot(arc_xs, arc_ys, colour = 'red', lw = three)
plt.gca().annotate('Arc', xy=(1.5, 0.4), xycoords='data', fontsize=10, rotation = 120)                    plt.xlim(-two, 2)
plt.ylim(-ii, 2)
plt.gca().set_aspect('equal')
plt.evidence()        

Output:

Arc

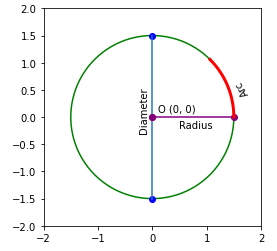
Draw radius from 0 to pi/4 and complete the arc

          plt.figure(figsize = (xviii, 7))          #depict point at orgin
plt.plot(0,0, color = 'blood-red', marker = 'o')
plt.gca().annotate('O (0, 0)', xy=(0 + 0.1, 0 + 0.1), xycoords='data', fontsize=10)          #depict circumvolve
r = one.5
angles = linspace(0 * pi, 2 * pi, 100 )
xs = r * cos(angles)
ys = r * sin(angles)          plt.plot(xs, ys, color = 'greenish')          #draw daimeter
plt.plot(0, i.5, marker = 'o', color = 'blueish')
plt.plot(0, -i.5, marker = 'o', color = 'blue')
plt.plot([0, 0], [1.v, -1.5])
plt.gca().annotate('Diameter', xy=(-0.25, -0.25), xycoords='data', fontsize=10, rotation = 90)          #depict radius
#plt.plot(0, 0, marking = 'o', color = 'royal')
plt.plot(1.5, 0, marker = 'o', color = 'purple')
plt.plot([0, 1.5], [0, 0], color = 'purple')
plt.gca().annotate('Radius', xy=(0.5, -0.2), xycoords='information', fontsize=10)          #draw arc
arc_angles = linspace(0 * pi, pi/iv, 20)
arc_xs = r * cos(arc_angles)
arc_ys = r * sin(arc_angles)
plt.plot(arc_xs, arc_ys, colour = 'red', lw = 3)
plt.gca().annotate('Arc', xy=(1.5, 0.4), xycoords='information', fontsize=10, rotation = 120)                      #draw another radius
plt.plot(r * cos(pi /4), r * sin( pi / four), marker = 'o', color = 'ruby-red')
plt.plot([0, r * cos(pi /4)], [0, r * sin( pi / 4)], color = "purple")                    plt.xlim(-2, 2)
plt.ylim(-2, ii)
plt.gca().set_aspect('equal')
plt.show()        

Output:

Arc

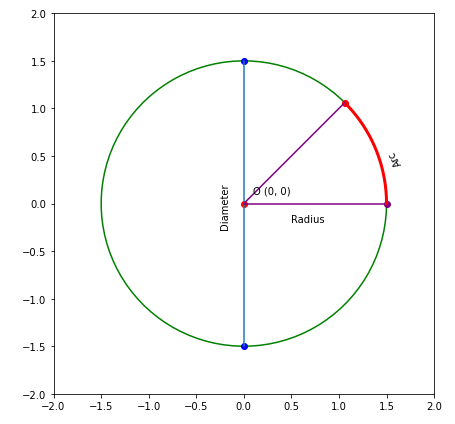
Write annotation of arc

          plt.figure(figsize = (xviii, 7))          #draw indicate at orgin
plt.plot(0,0, color = 'red', marking = 'o')
plt.gca().annotate('O (0, 0)', xy=(0 - 0.1, 0 + 0.1), xycoords='data', fontsize=10)          #draw circle
r = i.5
angles = linspace(0 * pi, 2 * pi, 100 )
xs = r * cos(angles)
ys = r * sin(angles)          plt.plot(xs, ys, color = 'green')          #describe daimeter
plt.plot(0, ane.5, marking = 'o', color = 'blue')
plt.plot(0, -1.5, marker = 'o', color = 'blue')
plt.plot([0, 0], [1.v, -one.5])
plt.gca().comment('Diameter', xy=(-0.25, -0.25), xycoords='data', fontsize=10, rotation = 90)          #depict radius
#plt.plot(0, 0, marker = 'o', color = 'regal')
plt.plot(1.5, 0, marker = 'o', color = 'purple')
plt.plot([0, one.5], [0, 0], color = 'purple')
plt.gca().annotate('Radius', xy=(0.5, -0.two), xycoords='data', fontsize=10)          #draw arc
arc_angles = linspace(0 * pi, pi/4, twenty)
arc_xs = r * cos(arc_angles)
arc_ys = r * sin(arc_angles)
plt.plot(arc_xs, arc_ys, color = 'red', lw = 3)
            #plt.gca().annotate('Arc', xy=(1.five, 0.4), xycoords='data', fontsize=ten, rotation = 120)
plt.gca().comment(r'Arc = r * $\theta$', xy=(1.three, 0.iv), xycoords='data', fontsize=10, rotation = 120)                    #draw another radius
plt.plot(r * cos(pi /four), r * sin( pi / four), marker = 'o', color = 'red')
plt.plot([0, r * cos(pi /iv)], [0, r * sin( pi / 4)], color = "purple")                      # depict theta angle and annotation
r1 = 0.5
arc_angles = linspace(0 * pi, pi/iv, 20)
arc_xs = r1 * cos(arc_angles)
arc_ys = r1 * sin(arc_angles)
plt.plot(arc_xs, arc_ys, colour = 'green', lw = 3)
plt.gca().comment(r'$\theta$', xy=(0.5, 0.2), xycoords='data', fontsize=15, rotation = 90)
plt.gca().annotate('<----- r = ane.5 ---->', xy=(0 - 0.ii, 0 + 0.2), xycoords='data', fontsize=fifteen, rotation = 45)                    plt.xlim(-ii, 2)
plt.ylim(-ii, 2)
plt.gca().set_aspect('equal')
plt.show()        

Output:

Arc with annotation

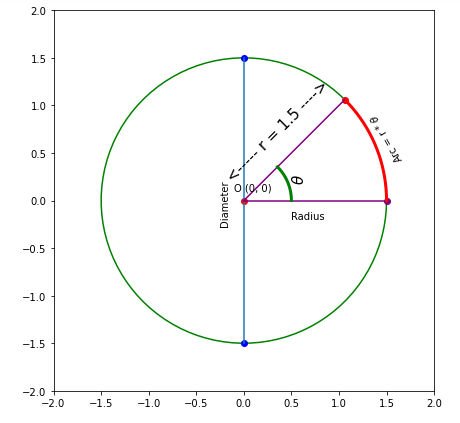
Draw segment(chord)

          plt.figure(figsize = (xviii, 7))          #draw point at orgin
plt.plot(0,0, color = 'red', mark = 'o')
plt.gca().annotate('O (0, 0)', xy=(0 - 0.i, 0 + 0.ane), xycoords='data', fontsize=10)          #draw circle
r = 1.v
angles = linspace(0 * pi, 2 * pi, 100 )
xs = r * cos(angles)
ys = r * sin(angles)          plt.plot(xs, ys, color = 'green')          #depict daimeter
plt.plot(0, 1.five, marker = 'o', color = 'bluish')
plt.plot(0, -1.5, marker = 'o', color = 'bluish')
plt.plot([0, 0], [ane.5, -i.5])
plt.gca().comment('Diameter', xy=(-0.25, -0.25), xycoords='data', fontsize=10, rotation = 90)          #depict radius
#plt.plot(0, 0, mark = 'o', color = 'purple')
plt.plot(1.5, 0, mark = 'o', color = 'regal')
plt.plot([0, 1.5], [0, 0], color = 'royal')
plt.gca().annotate('Radius', xy=(0.5, -0.ii), xycoords='data', fontsize=10)          #depict arc
arc_angles = linspace(0 * pi, pi/4, 20)
arc_xs = r * cos(arc_angles)
arc_ys = r * sin(arc_angles)
plt.plot(arc_xs, arc_ys, color = 'ruby', lw = 3)
#plt.gca().annotate('Arc', xy=(1.v, 0.iv), xycoords='data', fontsize=10, rotation = 120)
plt.gca().annotate(r'Arc = r * $\theta$', xy=(1.3, 0.4), xycoords='data', fontsize=10, rotation = 120)          #draw some other radius
plt.plot(r * cos(pi /iv), r * sin( pi / 4), marker = 'o', color = 'carmine')
plt.plot([0, r * cos(pi /4)], [0, r * sin( pi / 4)], color = "purple")          # draw theta bending and annotation
r1 = 0.5
arc_angles = linspace(0 * pi, pi/4, 20)
arc_xs = r1 * cos(arc_angles)
arc_ys = r1 * sin(arc_angles)
plt.plot(arc_xs, arc_ys, colour = 'green', lw = 3)
plt.gca().comment(r'$\theta$', xy=(0.5, 0.two), xycoords='data', fontsize=15, rotation = 90)
plt.gca().comment('<----- r = 1.5 ---->', xy=(0 - 0.ii, 0 + 0.2), xycoords='data', fontsize=xv, rotation = 45)                      #draw segment
r2 = 1.v
segment_angles = linspace(3/iv * 2* pi, 2 * pi, 100 )
segment_xs = r2 * cos(segment_angles)
segment_ys = r2 * sin(segment_angles)                                plt.plot(segment_xs, segment_ys, color = 'yellow')                                plt.plot([ane.v, 0], [0, -i.5], color = 'yellow')
plt.gca().annotate('Segment', xy=(0.5, -1.two), xycoords='data', fontsize=15, rotation = 45)
seg_x_p1 = r2 * cos(ii * pi)                    plt.xlim(-2, 2)
plt.ylim(-2, two)
plt.gca().set_aspect('equal')
plt.testify()        

Output:

Segment(chord)

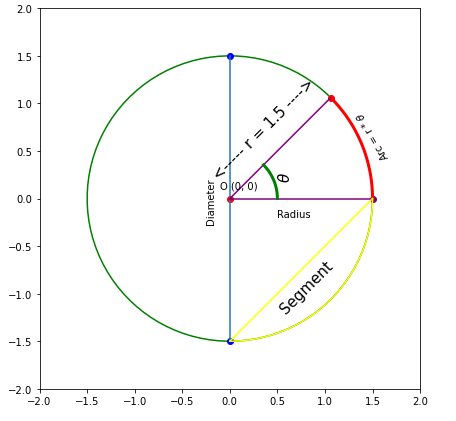
That's information technology. Thanks for reading.

allredmothasaim.blogspot.com

Source: https://medium.com/@nutanbhogendrasharma/draw-circle-diameter-radius-arc-and-segment-using-python-matplotlib-module-343705417622

Share this post